Preface

This research contains as a main result the prove that every Chordal B₁-EPG graph is simultaneously in the graph classes VPT and EPT. In addition, we describe a set of graphs that define Helly-B₁-EPG families. In particular, this work presents some features of non-trivial families of graphs properly contained in Helly-B₁ EPG, namely Bipartite, Block, Cactus and Line of Bipartite graphs.

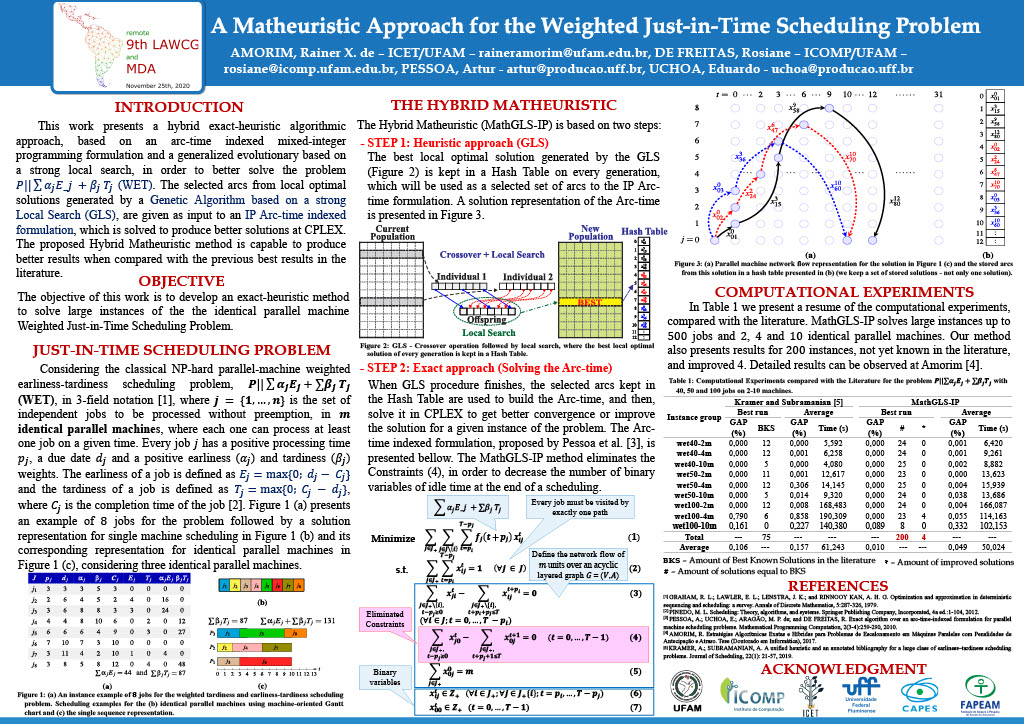
This work presents a hybrid exact-heuristic algorithmic approach, based on an arc-time indexed mixed-integer programming formulation and a generalized evolutionary based on a strong local search, to better solve classical parallel machine scheduling problems involving weighted tardiness and weighted earliness-tardiness penalties, with independent jobs and arbitrary processing times. Thus, the proposed method of this research is based on two steps. In the first step, some selected arcs from local optimal solutions, generated by a Genetic Algorithm based on a strong Local Search with generalized pairwise interchanges (GLS), are given as input to an integer programming formulation. In the second step, in order to produce improved solutions, the exact-full IP formulation is solved at CPLEX with the selected arcs from GLS. The computational experiments present competitive results when compared with the previous best results of the literature, including large instances up to 500 jobs on 2-10 identical parallel machines.

This paper presents an exact method for the Wireless Sensor Network Planning Problem with Multiple Sources/Destinations (WSNDP-MOD). In this work, we want to minimize the number of sensors in the network topology in a given region of interest, in order to balance data traffic between multiple sources and destinations. To solve the proposed problem, we will define an Integer Programming model and an auxiliary graph that will be used with the model. Computational experiments were performed using a real topology.

We exhibit a way to obtain lower bounds on the algebraic connectivity and on the log-Sobolev constant of a large class of graphs, for instance discrete approximations of fractals. We illustrate the method obtaining upper bounds on the inverse of both parameters on the Hanoi graphs. Our results imply upper bounds on the time that the random walk on the configurations of the tower of Hanoi puzzle, with 3 towers and m disks, gets lost.

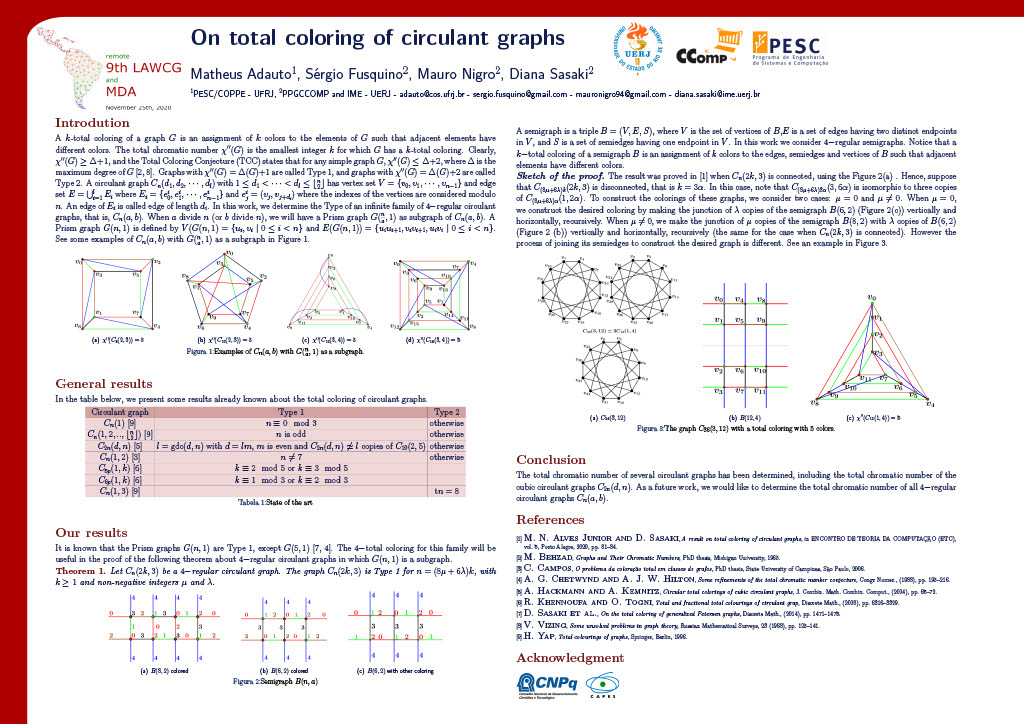
A k-total coloring of a graph G is an assignment of k colors to the elements of G such that adjacent elements have different colors. The total chromatic number χ''(G) is the smallest integer k for which G has a k-total coloring. Clearly, χ''(G)≥ Δ+1, and the Total Coloring Conjecture (TCC) states that for any simple graph G, the total chromatic number is either Δ(G) + 1 (graphs are called Type 1) or Δ(G) + 2 (graphs are called Type 2). In this work, we determine the total chromatic number of all members of an infinite family of 4-regular circulant graphs.

The search for counter examples to the Four Color Conjecture originated snarks, which are bridgeless cubic graphs with chromatic index 4. A total coloring of a graph G is an association of colors to the vertices and edges of G, so that adjacent or incident elements do not have the same colors. If the difference between cardinalities of any two colors is at most one, the coloring is said equitable. In this work we construct an equitable total coloring for the infinite family of snarks named Blowups.

A strict connection tree of a graph G for a non-empty subset W of V(G), called terminal set, is a tree subgraph of G whose leaf set is equal to W. A non-terminal vertex of a strict connection tree T is called linker if its degree in T is exactly 2, and it is called router if its degree in T is at least 3. The Strict Terminal Connection problem (S-TCP) has as input a graph G, a non-empty subset W of V(G) and two non-negative integers, and it asks whether G admits a strict connection tree for W with at most l linkers and at most r routers. In this work, we prove that S-TCP is NP-complete even if l is fixed and the input graph is restricted to chordal bipartite graphs.

Tuza (2017) contributed to the area of graph labeling presenting many results in his seminal paper and proposing new labeling games. We investigate the Range-Relaxed Graceful game (RRG game) and present a lower bound for the number of available labels for which Alice has a winning strategy in the RRG game on a simple graph G, on a cycle and on a path graph.

We compute the sandpile groups of outerplanar graphs. The method can be used to determine the algebraic structure of the sandpile groups of other planar graph families.

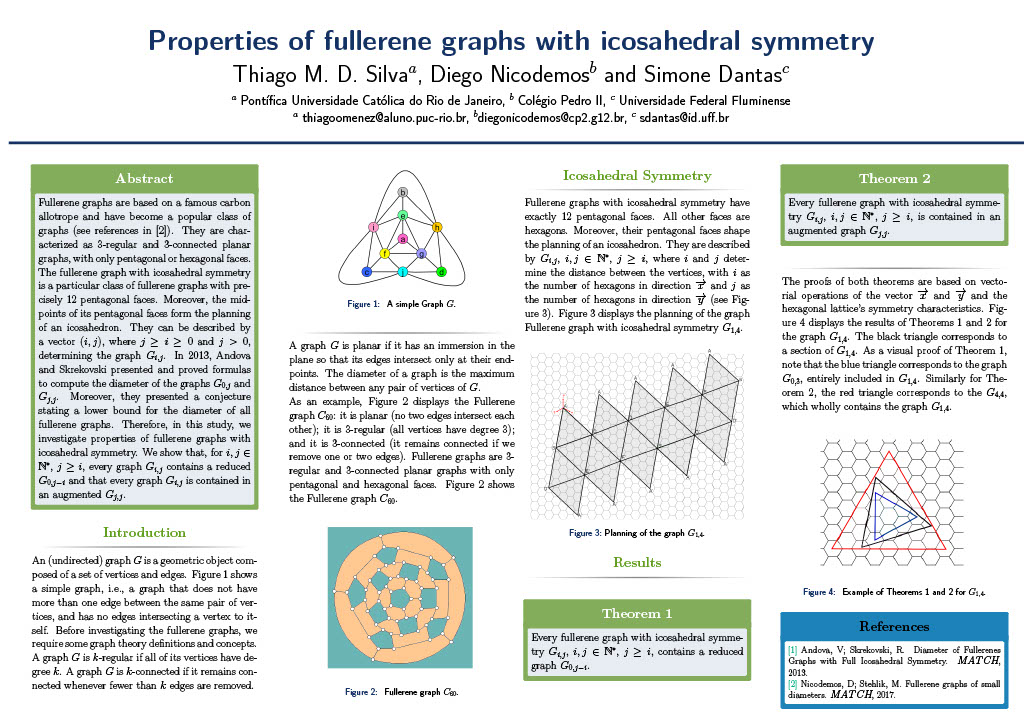
Fullerene graphs have become a popular class of graphs recently. They are characterized as 3-regular and 3-connected planar graphs, with only pentagonal or hexagonal faces. The fullerene graph with icosahedral symmetry is a particular class of fullerene graphs with precisely 12 pentagonal faces. Moreover, the midpoints of its pentagonal faces form the planning of an icosahedron. They can be described by a vector (i, j), determining the graph G_i,j. In 2013, Andova and Skrekovski presented and proved formulas to compute the diameter of the graphs G_{0, j} and G_{j, j}. Moreover, they presented a conjecture stating a lower bound for for the diameter of all fullerene graphs. Therefore, in this study, we investigate properties of fullerene graphs with icosahedral symmetry. We show that every graph G_{i, j} contains a reduced G_0,j-i and that every graph G_{i, j} is contained in an augmented G_{j, j}.

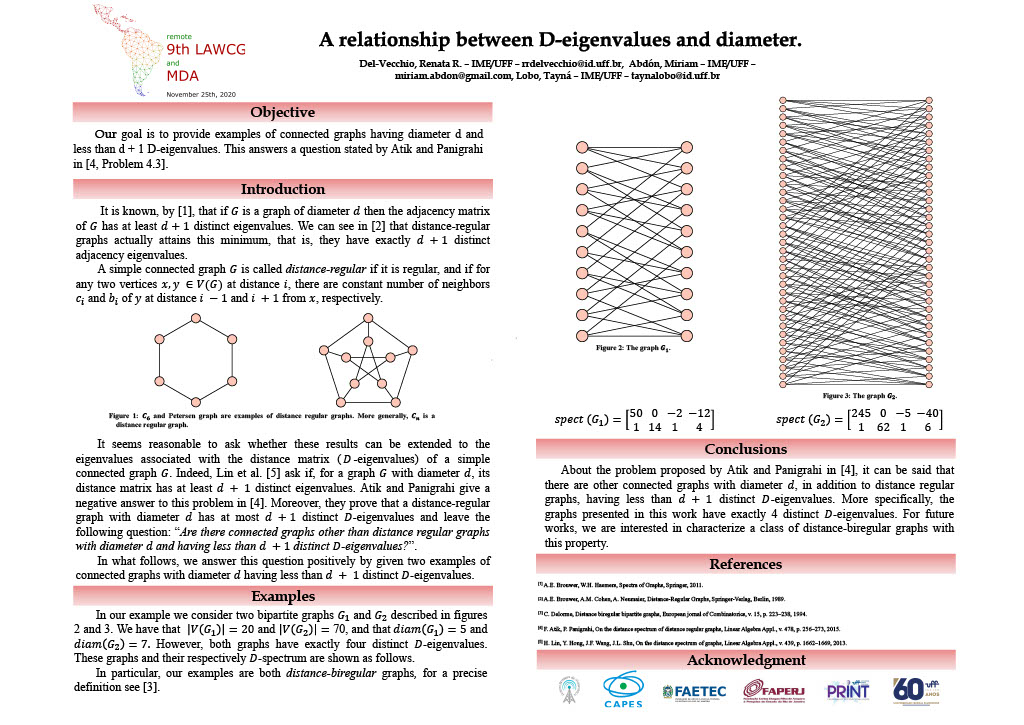
In this poster we provide examples of connected graphs (which are not distance-regular) having diameter d and such that its distance matrix has less than d + 1 eigenvalues (D-eigenvalues). This answers a question posed by Atik and Panigrahi in On the distance spectrum of distance regular graphs, Linear Algebra and its Applications, v. 478, p. 256–273, 2015.

In Cellular Networks, communication between bases and mobile devices is established via radio frequencies. Interference occurs if one particular device communicates with two different bases that have the same frequency. So, every device must contact a base with an unique frequency and, since having a lot of different frequencies is expensive, it’s important trying to minimize their quantity, in a way that there exists no interference. With that motivation, in 2002, Even, Lotker, Ron and Smorodinsky introduced the concept of Conflict Free coloring in a geometric scenario, which itself led to the study of Conflict Free Closed Neighborhood (CFCN) coloring in graphs. Inspired by this problem and by the well known coloring game, we introduce a game theoretical approach to CFCN coloring, and determine the minimum number of colors necessary for Alice to have a winning strategy in the case of Complete Graphs.

The teaching of Combinatorial Analysis is still done in a very mechanical way by some teachers who memorize formulas without a real content domain. This practice is repeated superficially and does not stimulate combinatorial reasoning. In this work, we show how Newton's Binomial is presented in Genetics, as a contribution to the teaching of the algebraic expansion of powers of a binomial.

A vertex coloring of a graph G is a strong pseudoachromatic coloring if there are adjacent vertices colored i and j for every two colors i and j, distinct or not. The maximum number of colors for a strong pseudoachromatic coloring of a graph G is the strong pseudoachromatic number, ψ*(G). Liu, Li, and Liu (2015) present upper and lower bounds for ψ*(G) and determine ψ*(G) when G is a complete graph, a path, a cycle, a complete multipartite graph, a complete biequipartite graph from which a perfect matching is deleted, a wheel, or a fan. We observe that ψ*(G) = α'(G) for complete graphs and multipartite graphs, where α'(G) is the size of a maximum matching of G, and pose the question of which other graph classes have ψ*(G) = α'(G). We prove that split graphs is one of these classes.

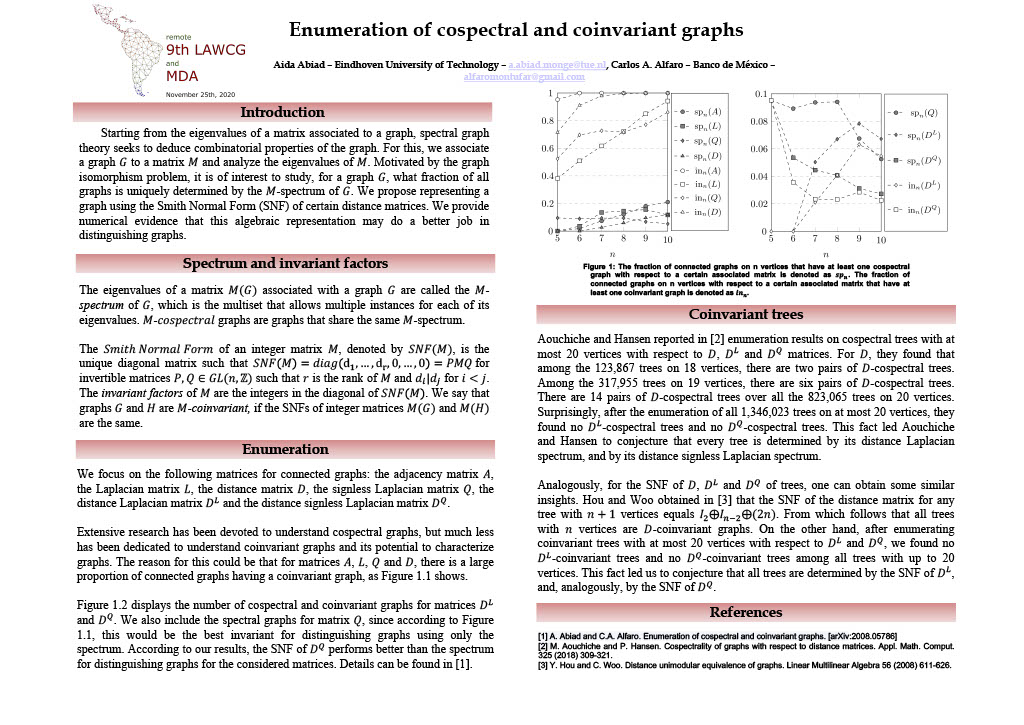
We present enumeration results on the number of connected graphs up to 10 vertices for which there is at least one other graph with the same spectrum (cospectral mate), or at least one other graph with the same Smith Normal Form (coinvariant mate) with respect to several matrices associated to a graph. The presented numerical data give some indication that possibly the Smith Normal Form of the distance Laplacian and the distance signless Laplacian matrices could be a finer invariant than the spectrum for distinguishing graphs.

The (proper) thinness of a graph is a width parameter that generalizes (proper) interval graphs, which are exactly the graphs of (proper) thinness one, and graphs with thinness two include bipartite convex graphs. Many NP-complete problems can be solved in polynomial time given a thin representation of bounded size. It is known that the thinness of a graph is at most its pathwidth plus one, and we prove that the proper thinness of a graph with at least one edge is at most its bandwidth. Another known result is that boxicity is a lower bound for thinness. The main result of this work are characterizations of (proper) 2-thin graphs as intersection graphs of rectangles in the plane, with appropriate conditions. An alternative characterization leads to showing that 2-thin graphs are L-graphs (thus B₁-VPG), and 3-thin graphs are B₃-VPG. It is also shown that B₀-VPG graphs may have arbitrarily large thinness.

The rainbow connection number of a connected graph G is the least k for which G admits a (not necessarily proper) k-edge-coloring such that between any pair of vertices there is a path whose edge colors are all distinct. This parameter has important applications. We present a near-tight bound for the rainbow connection number of snake graphs, a class commonly studied in labeling problems.

A total coloring is an assignment of colors to the vertices and edges of a graph G such that no two adjacent or incident elements receive the same color. The minimum number of colors for a total coloring of G is the total chromatic number, χ''(G). In the year that Celina Figueiredo, João Meidanis and Célia de Mello celebrate another decade of life, we prove an immediate consequence of their papers: all reduced indifference graphs have χ''(G) = Δ(G)+1.

We are interested in embedding trees T with maximum degree at most 4 in a rectangular grid, such that the vertices of T correspond to grid points, while edges of T correspond to non-intersecting straight segments of the grid lines. The aim is to minimize the maximum number of bends of a path of T. We provide a quadratic-time algorithm for this problem. By applying this algorithm, we obtain an upper bound on the number of bends of EPG representations of graphs that are in both the classes of VPT and EPT.

In this paper, we are interested in the edge intersection graphs of paths of a grid where each path has at most one bend, called B₁-EPG graphs and first introduced by Golumbic et al (2009). We also consider a proper subclass of B₁-EPG, the L-EPG graphs, which allows paths only in “L” shape. We show that two superclasses of trees are B₁-EPG (one of them being the cactus graphs). On the other hand, we show that the block graphs are L-EPG and provide a linear time algorithm to produce L-EPG representations of generalization of trees. These proofs employed a new technique from previous results based on block-cutpoint trees of the respective graphs.

An ⌞-graph is a vertex intersection graph of paths in a grid such that all the paths in the representation have the shapes {|,_,⌞}. We will say that the graph is an strict ⌞-graph if the paths only have the shape ⌞. An (strict) ⌞-contact graph is an (strict) ⌞-graph such that all the paths in the representation do not cross each other and do not share an edge of the grid. The class of planar Laman graphs is of interest due to the fact that it contains several large classes of planar graphs. It was shown that planar Laman graphs are strict ⌞-contact graphs but using all four rotations of ⌞. In this work we study relations between (strict) ⌞-graphs and planarity. We also present a minimal forbidden induced subgraph characterization of strict ⌞-contact graphs within the class of chordal graphs.

A square-complementary graph is a graph such that its square and its complement are isomorphic. Here, we provide a computer-assisted proof showing that there are no 4-regular square graphs of girth greater than 4, thus solving in the negative an open problem in Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. 5 (1994) 43-48, and also in Discrete Mathematics 327 (2014) 62-75.

A total coloring for a graph G is an assignment of colors to the edges and vertices of G, such that any pair of adjacent or incident elements have different colors. The least number of colors for which G has a total coloring is denoted χ''(G). It is known that split-comparability graphs have χ''(G) at most Δ(G)+2. In this work we show that certain split-comparability graphs with odd maximum degree have χ''(G) = Δ(G) + 1.

An L(2,1)-labeling of a graph G is a function f: V(G)→ [0, t] such that |f(u) - f(v)| ≥ 2 if d(u,v) = 1, and f(u) ≠ f(v) if d(u,v) = 2, for u,v ∈ V(G). The span of an L(2,1)-labeling is the largest integer t used. An L(2,1)-labeling of G is optimal when it has the smallest possible span and such a value is denoted by λ(G). Georges and Mauro explored the problem of determining λ(G) for 3-regular graphs. The authors conjectured that, with the exception of the Petersen Graph, every connected 3-regular graph G has λ(G) ≤ 7. In this work, we verify Georges and Mauro's Conjecture for Loupekine Snarks and we present a lower bound on λ(G) for the members of this family of graphs.

In this work, we describe an algorithm to determine optimal two level Hamming-Huffman trees when the symbols have uniform frequencies. That is, the algorithm builds optimal Hamming-Huffman trees in which all leaves lay in at most two different levels. Also, considering experimental results, we conjecture that, for uniform frequencies, optimal two levels Hamming-Huffman trees are optimal in general.

A graph is a mathematical model used to represent relationships between objects. The general characters that both of these objects and its relationships can assume, allowed the construction of the so-called Graph Theory, which has been applied to model problems in several areas, such as Mathematics, Physics, Computer Science, Engineering, Chemistry, Psychology and industry. Most of them are large scale problems. Fullerene graphs are mathematical models for carbon-based molecules experimentally discovered in the early 1980s by Kroto, Heath, O’Brien, Curl and Smalley. Many parameters associated with these graphs have been discussed to describe the stability of Fullerene molecules. By definition, Fullerene graphs are cubic, planar, 3-connected with pentagonal and hexagonal faces. The motivation of the present study is to find an efficient method to obtain a 4-total coloring of a particular class of Fullerene graphs named Fullerene nanodiscs, if it exists.

This work aims at presenting the uniformly clique-expanded graphs and its results on global defensive alliance and total dominating set problems. Those graphs are related to Sierpiński graphs (KLAVŽAR et. al, 2002) and subdivided-line graphs (HASUNUMA, 2013). We show the minimum cardinality of the global defensive alliance for some particular situations of uniformly clique-expanded graphs, and we also relate that cardinality to the total dominating set number for graphs having a path or cycle as the root.

The annihilation number is a graph invariant used as a sharp upper bound for the independence number. In this work, we present bounds and Nordhaus-Gaddum type inequalities for the annihilation number. We also investigate the extremal behavior of the invariant and showed that both parameters satisfy the interval property. In addition, we characterize some extremal graphs, ensuring that the bounds obtained are the best possible.

Un vértice de un grafo se domina a sí mismo y a todos sus vértices adyacentes. Para un grafo G = (V;E) y un número entero positivo k, un conjunto k-upla dominante en G es un subconjunto D ⊆ V tal que todo vértice en V es dominado por al menos k elementos de D. El problema de la k-upla dominación consiste en hallar un conjunto k-upla dominante en G de mínimo tamaño (γ_k(G)). Este problema es NP-difícil. Estudiamos subclases de grafos arco-circulares, en los cuales la complejidad de este problema no es conocida para k≠1. En un trabajo previo exploramos la subclase de los grafos concave-round, habiendo comenzado nuestro estudio sobre los grafos web. Obtuvimos γ_k(W) para todo grafo web W. En este poster mostramos el diseño de un algoritmo lineal que devuelve un conjunto k-upla dominante de tamaño γ_k(W) para todo k y grafo web.

Uma rotulação ℒ (h, k) de um grafo simples G é uma atribuição de inteiros não-negativos aos vértices de G tal que a diferença entre os rótulos de vértices adjacentes é pelo menos h, e de vértices que tenham um vizinho em comum é pelo menos k. O span de G é o menor inteiro t para o qual G admite uma rotulação ℒ (h, k) em que a diferença entre os rótulos de quaisquer dois vértices é no máximo t. Neste trabalho, determinamos o span dos Sunlets, que são os grafos obtidos a partir dos ciclos adicionando-se um pingente a cada vértice.

Neste trabalho, investiga-se a existência de emparelhamento perfeito no produto cartesiano de duas árvores sem emparelhamento perfeito, com foco no caso de árvores do tipo caterpillar. Especificamente, é descrita uma família infinita de caterpillars com um número par de vértices e sem emparelhamento perfeito, tais que o produto cartesiano de duas quaisquer destas árvores possui emparelhamento perfeito.

Graph matching problems are well known and studied, in which we want to find sets of pairwise non-adjacent edges. This work focus on the study of matchings that induce subgraphs with special properties. For this work, we consider the property of being connected, also studying it for weighted or unweighted graphs. For the unweighted ones, we want to obtain a matching with the maximum cardinality, while for the weighted graphs, we look for a matching whose sum of the matching edge weights is maximum. The problem of maximum connected matching is polynomial. We show ideas that lead to two linear algorithms. One of them, having a maximum matching as input, determines an maximum unweighted connected matching. The complexity of the maximum weighted connected matching problem is unknown for general graphs. However, we present a linear time algorithm that solves it for trees.

In this work, we study a subclass of the family of matrogenic graphs. This family is little known in the literature, and does not yet have its determined laplacian spectrum. With the intention of beginning the study on the laplacian spectrum of this family, we will show the spectrum of a subclass contained therein, and then using the Matrix-Tree Theorem, its number of spanning trees.

An s-branching flow f in a network N = (D,c) (where c is the capacity function) is a flow that reaches every vertex in V(D) - s from s while loosing exactly one unit of flow in each vertex other than s. In other words, for a vertex v ∈ V(D) - s, the difference between the flow entering and leaving v is one. We further investigate a conjecture proposed by Costa et. al (2019) that aims to characterize networks admitting k arc-disjoint s-branching flows, generalizing a result that provides such characterization when all arcs have capacity n-1, based on Edmonds' branching Theorem. We show that, in general, the conjecture is false. However, it holds for out-branchings with parallel arcs.

The independence gap of a graph G is the difference between the maximum and the minimum sizes of a maximal independent set in G. We present a characterization of graphs with independence gap at least 1 that are of girth at least 6 with exactly two support vertices having exactly r leaves. We also present results related to the number of trees with specific sizes of maximal independent sets.

In this work, our objective is to characterize classes of graphs with up to four 3-cuts that admit a 3-flow. K₄, the complete graph on four vertices, is the smallest bridgeless graph that does not admit a 3-flow. We focus on almost even graphs, i.e., bridgeless graphs with up to six odd vertices. We obtain a characterization for almost even graphs with up to four odd vertices. We also obtain a partial characterization for almost even graphs with up to four 3-vertices (vertices of degree three) and two odd vertices of higher degree.

The subset S is k-independent if the maximum degree of the subgraph induced by the vertices of S is at most k − 1. We present sharp lower and upper bounds for maximum 2-independent sets in complementary prism of any graph, characterize the graphs for which the upper and lower bound holds, and present closed formulas for the complementary prism of paths, cycles and complete graphs.

There are algorithms that use the branch and bound technique for Maximum Clique Problem (CM) and Vertex Coloring as the upper bound. The algorithm known as Lexicographic Breadth-first Search (LexBFS) is capable of producing vertex ordering of some graph classes that lead to the solution of difficult problems in polynomial time. The aim of this work is to study branch and bound algorithms that use vertex coloring to solve CM modified with the LexBFS. Methods of Experimental Analysis of Algorithms were used to evaluate changes. It was possible to make inferences about the results obtained using the statistical method of hypothesis testing. The conclusion is that in instances of graphs considered the search space is smaller, but the execution time was longer. When evaluating with generated random instances, both the search space and the execution time were significantly shorter for some algorithms.

In the Multicolored Independent Set problem, we are given a graph G and a partition of V(G) into k sets, and the goal is to find an independent set of G that hits each part exactly once. Along with Independent Set, Clique, and Multicolored Clique, Multicolored Independent Set is one of the most widely used problems in lower bound proofs in parameterized complexity. While all four are known to be fixed-parameter tractable when parameterized by vertex cover, only the latter had no kernelization results. We fill this gap by using the cross-composition framework of Bodlaender et al. [STACS 2011] to show that Multicolored Independent Set has no polynomial kernel when parameterized by distance to any non-trivial graph class and size of the solution, unless NP is contained in coNP/poly.

The Partitioning Graphs into Monochromatic Trees problem (PGMT) consists of partitioning an edge-colored graph into vertex disjoint monochromatic trees. It has been known that PGMT is NP-Complete. In this work we consider some particular cases of this problem, where the number of occurrences of each color is bounded by a constant f. We show that this new version is NP-Complete even for f = 3.

Let G be a connected graph of order n, A(G) the adjacency matrix of G and D(G) the diagonal matrix of the row-sums of A(G). For every real α in [0,1], Nikiforov defined the matrix A_α(G) as A_α(G)=αD(G)+(1- α)A(G). In this work, we show a factorization of the A_α-characteristic polynomial of a family of matrogenic graphs.

A locally irregular graph is a graph in which adjacent vertices have distinct degrees. A locally irregular k-coloring, or k-LIC, for short, of a graph G is a coloring of E(G) in which every color class induces a locally irregular subgraph. Baudon, Bensmail, Przybyło, and Woźniak, (2015) conjectured that if a graph G admits a k-LIC, then G admits a 3-LIC. In this work we verify this conjecture for a family of cubic graphs, and we present a condition for graphs not to admit a 2-LIC.

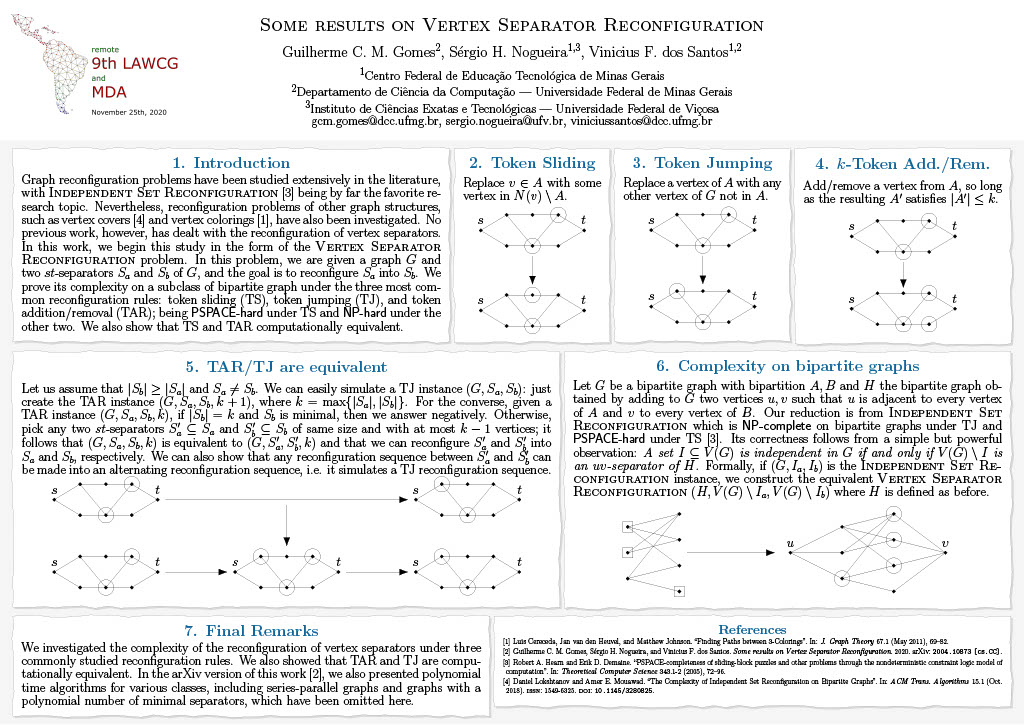
We present the first results on the complexity of the reconfiguration of vertex separators under the three most popular rules: token addition/removal, token jumping, and token sliding. We show that, aside from some trivially negative instances, the first two rules are equivalent to each other and that, even if only on a subclass of bipartite graphs, token sliding is not equivalent to the other two unless NP = PSPACE; we do this by showing a relationship between separators and independent sets in this subclass of bipartite graphs, which implies that Vertex Separator is NP-hard under token jumping and PSPACE-hard under token sliding.

We introduce a concept of packing of graphs which generalizes all those previously defined in the literature and we study the computational complexity of computing the associated parameter, the generalized packing number of the graph. We find that this new packing parameter comes to be much more complicated to handle than those previously defined, even on particular graph classes as spider and quasi-spider graphs. Nevertheless, we prove that the associated optimization problem can be solved in linear time for some graph classes with few P₄'s.

Um conjunto dominante total de um grafo G=(V, E), é um subconjunto D de V(G) tal que |N(v) ∩ D| ≥ 1, para todo v ∈ V(G). E um conjunto independente aberto de um grafo G é um conjunto S de vértices de G, tal que |N(v) ∩ S| ≤ 1, para cada v ∈ S. Neste trabalho apresentamos resultados sobre o número de dominação total e independência aberta para o produto lexicográfico de grafos gerais e para classes simples como os ciclos C_n, caminhos P_n e completos K_n.

The recognition of biclique graphs in general is still open. Recently, Groshaus and Guedes introduced the mutually included biclique graph as an intermediate operator to define the biclique graph. Also, we previously studied the biclique graph of interval bigraphs and proper interval bigraphs. In this work, we extend the results to a superclass, the interval containment bigraphs, in the context of the mutually included biclique graphs.

Reconfiguration problems focus on transforming a state of a combinatorial or geometric object into another by performing some sequence of operations. In one important class of reconfiguration problems, valid moves consist on moving items along the edges of a graph to achieve a desired final configuration. The Token Swapping (TS) problem is one of these problems and is known to be NP-hard. This work introduces the reader to the approach of solving this problem by an integer linear program model and present an efficient algorithm for solving the TS problem on complement-reducible graphs, also called cographs.

Consider a graph G=(V,E) and a subset C of V. The P₃-convex hull (resp. P₃*-convex hull) of C is obtained by iteratively adding vertices with at least two neighbors (two non-adjacent neighbors) in C. A subset S of V is P₃-Helly-independent (P₃*-Helly-independent) when the intersection of the P₃-convex hulls (P₃*-convex hulls) of S\{v} (∀ v ∈ S) is empty. The P₃-Helly number (P₃*-Helly number) is the size of a maximum P₃-Helly-independent (P₃*-Helly-independent). The edge counterparts of P₃-Helly-independent and P₃*-Helly-independent of a graph follow the same restrictions applied to its edges. In this work, we established the edge P₃*-Helly number of grid graphs G(p×q) when both p and q are larger than 15. Moreover, we give partial results on forbidden configurations of edge P₃-Helly independent sets for these graphs.

The recognition of biclique graphs in general is still open. In recent years we presented some result on the characterization of biclique graphs of graphs of certain graph classes, along with the complexity associated to the recognition problem. Those results introduced some intermediate operators, which we call now as "functors". In this work we summarize all those results and organize the different approaches using the functors.

A bipartite graph is a circular arc bigraph if there exists a bijection between its vertices and a family of arcs on a circle such that vertices of opposing partite sets are neighbors precisely if their corresponding arcs intersect. The class is a relatively unexplored subject, with most results on it and its subclasses being quite recent. In our work, we provide a full exploration of the containment relations and intersections between seven subclasses of circular arc bigraphs.

The t-admissibility problem has been widely studied specially because determining if a graph G is 3-admissible is still an open problem since it was proposed. Although, recognizing if a graph is 2-admissible is a polynomial-time solvable problem, we realized that for some classes could be easier, so in this work we present simple and efficient algorithms in order to characterize 2 and 3-admissible graphs for some graph classes as cographs, split graphs, P₄-sparse and other superclasses.

In this poster we present some recent results about the Hamiltonicity of the 2-token graph, F₂(G), and the 2-multiset graph, M_k(G) of some fan graphs. As a consequence, we exhibit an infinite family of graphs for which F₂(G) and M₂(G) are Hamiltonian.